[Blog post published by the Communications of the ACM, August 27, 2020]
Last week, I was invited to deliver a keynote address for The Fourth International Conference on Computational Thinking Education 2020 (CTE2020) organized by the Education University of Hong Kong (EduHK). I was one of four keynote speakers (along with Hal Abelson of MIT, Marcus Specht of TU Delft, and Mario Piacentini of PISA/OECD). The topic of my keynote was CT in the Disciplines: Realizing the promise and potential of integrating computational thinking into school learning. A key aspect (and highlight) of my address was a conceptual framework that I presented, and explained, for integrating computing & CT into school subjects. The talk was well-received and I’ve received several requests since to share my slides. This blog post is an attempt to share the framework more broadly along with some detail—and give folks a reference to cite should they need to (before the article currently in review makes it out).
This framework has been in the making for some time now. I have been fortunate to get a good sense for several diverse CT integration projects (mainly in STEM subjects), having *led/co-led three STEM+C NSF grants that covered the gamut from Pre-K to high school (NSF #1543062, #1640199, #1639850); *collaborated with EDC to organize a 2-workshop series on “CT in the Disciplines”; *served as program committee member for the STEM+C PI Summit last fall (that was aimed at synthesis and dissemination); *co-edited a Special Issue for the Journal of Science Education and Technology (January 2020) focused on STEM+CT integration (with wonderful colleagues and partners in crime since the EDC workshops—Irene Lee, Fred Martin, Joyce Mayn-Smith, and Sarita Pillai) that produced a wonderful collection of 12 papers (I urge you all to read them!); *organized a STEM+C panel for SIGCSE 2020; *led a chapter (co-authored by Aman Yadav) on integrating programming into school subjects for the new A to Z Handbook on Teaching Programming, and finally, *brought together an AMAZING set of 50 researchers on 10 projects for an equally amazing symposium on CT/CS integration for ICLS 2020. (DO check out the slide deck here!)
My overwhelming sense from these experiences and attempts to synthesize CT/CS integration ideas is that we need a comprehensive conceptual framework for people who wish to understand or conceptualize integration—how to get started with designing for integration? what are all the considerations, dimensions, and elements? Researchers, teachers and designers typically turn to one or both of the following: (a) Elements of CT that are essentially derived from Jeannette Wing (2006), for example, Grover & Pea 2013 or Bocconi et al.(2017), that are rooted in computer science. Or they turn to Weintrop et al., 2016, a taxonomy of CT integration into Science and Math (largely) based on scientific and systems modeling research in Uri Wilensky’s lab. This taxonomy has proven to be useful for some STEM and CT integration efforts especially those involving computational modeling in science, but it is not universally applicable and it is not a framework. Often, neither of these (alone or together) is adequate.
A framework must allow us to develop and identify themes and constructs that would apply across diverse cases and examples of practice…Having a framework goes beyond merely identifying problems with current approaches; it offers new ways of looking at and perceiving phenomena and offers information on which to base sound, pragmatic decision making. – Mishra & Koehler, 2006
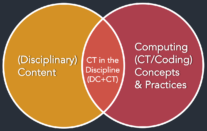
In order to imagine a framework for integration, I started with these two elements we had examined in the EDC workshops—CT and the discipline—to determine what CT looked like from a disciplinary perspective. What emerged from those workshops was what I believe is the WHY of CT integration, or what one gets out of integrating CT into the disciplines. However, it did not go far enough toward helping conceptualize the nitty gritty aspects of integration.
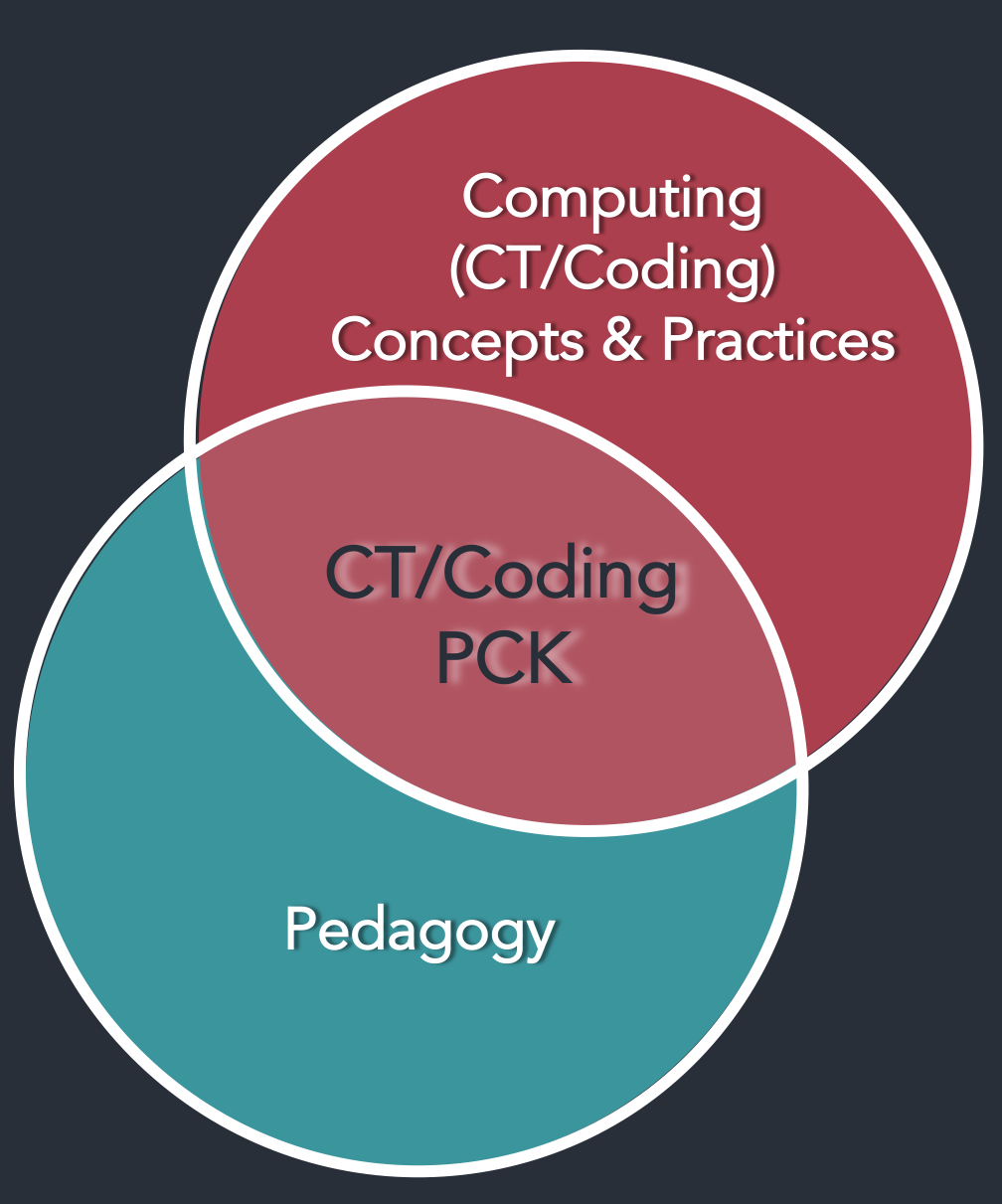
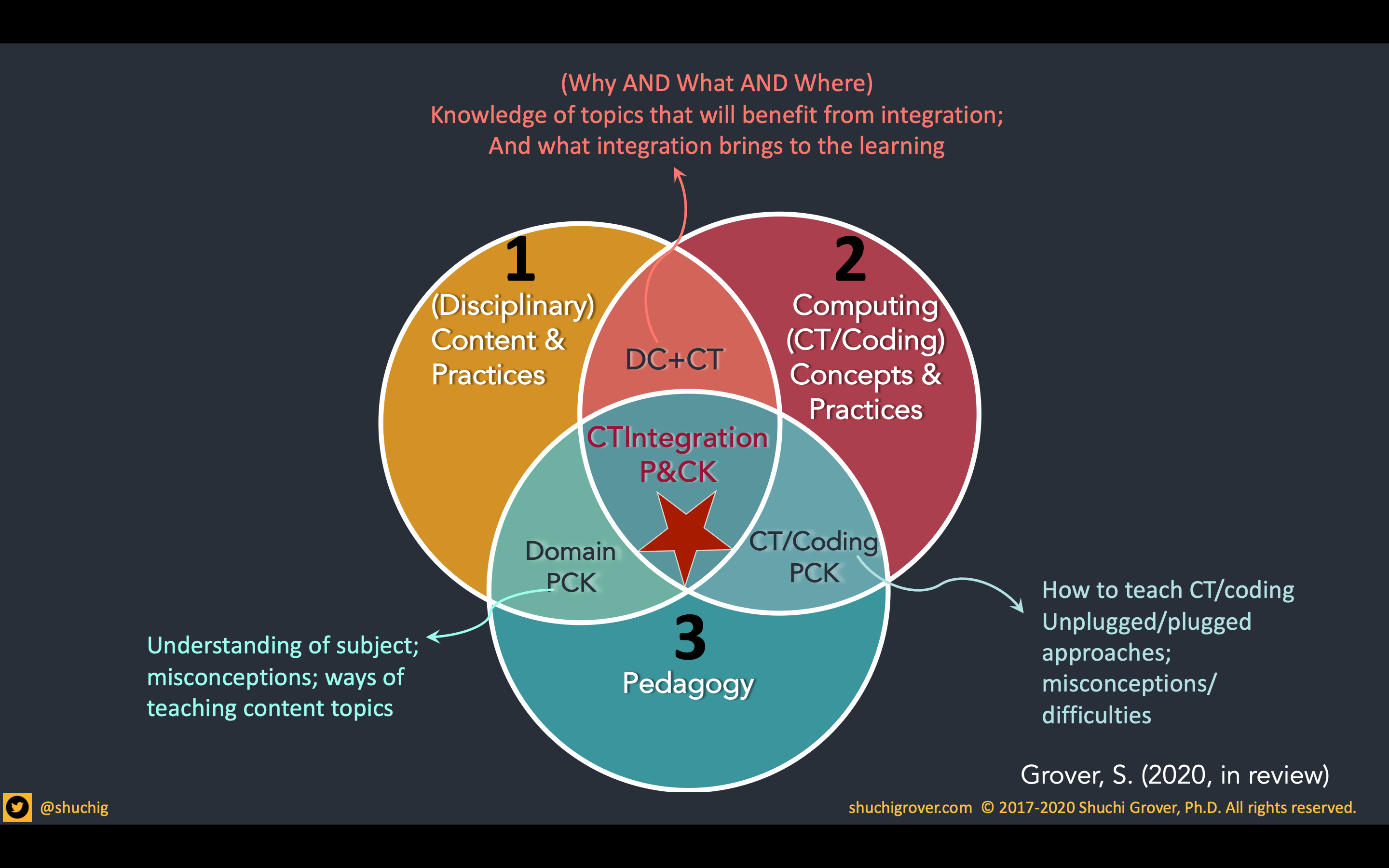What I discovered, though, was that adding a third element made a world of difference! And that third leg to balance out the framework was the all important element of pedagogy. It completely transformed the way one could conceptualize the HOW of integration of CT—that integration magic that happens at the center where all 3 circles intersect. With these three elements, we have not only domain knowledge, CT (concepts and practices) and their intersection, but pedagogy in general, and these 3 crucial new intersection spaces that involve pedagogy.
When we think about integration, we need to attend to 3 crucial intersections:
Domain PCK: The intersection of domain and pedagogy which we all know is of paramount importance when designing for instruction in any domain. It’s the understanding of the subject, and ways of teaching specific content topics based on known misconceptions and discipline-based education research.
CT/Coding PCK: This encompasses the vast body of CS ed research: all that we know about teaching coding and CT. Student misconceptions, pedagogy of programming, unplugged approaches, etc. All of this also plays an important role in integration contexts!
DC+CT: where we consider content and practices of the domain and of CS/CT, and their intersection. And here we need to go beyond thinking about the WHY of integration but also guidance on the WHAT & WHERE that was missing from the earlier product of the workshops. And these together contribute to guiding how to plan for integration, and making that CTIntegration magic happen at the center. However, we need a couple more considerations to complete the model!
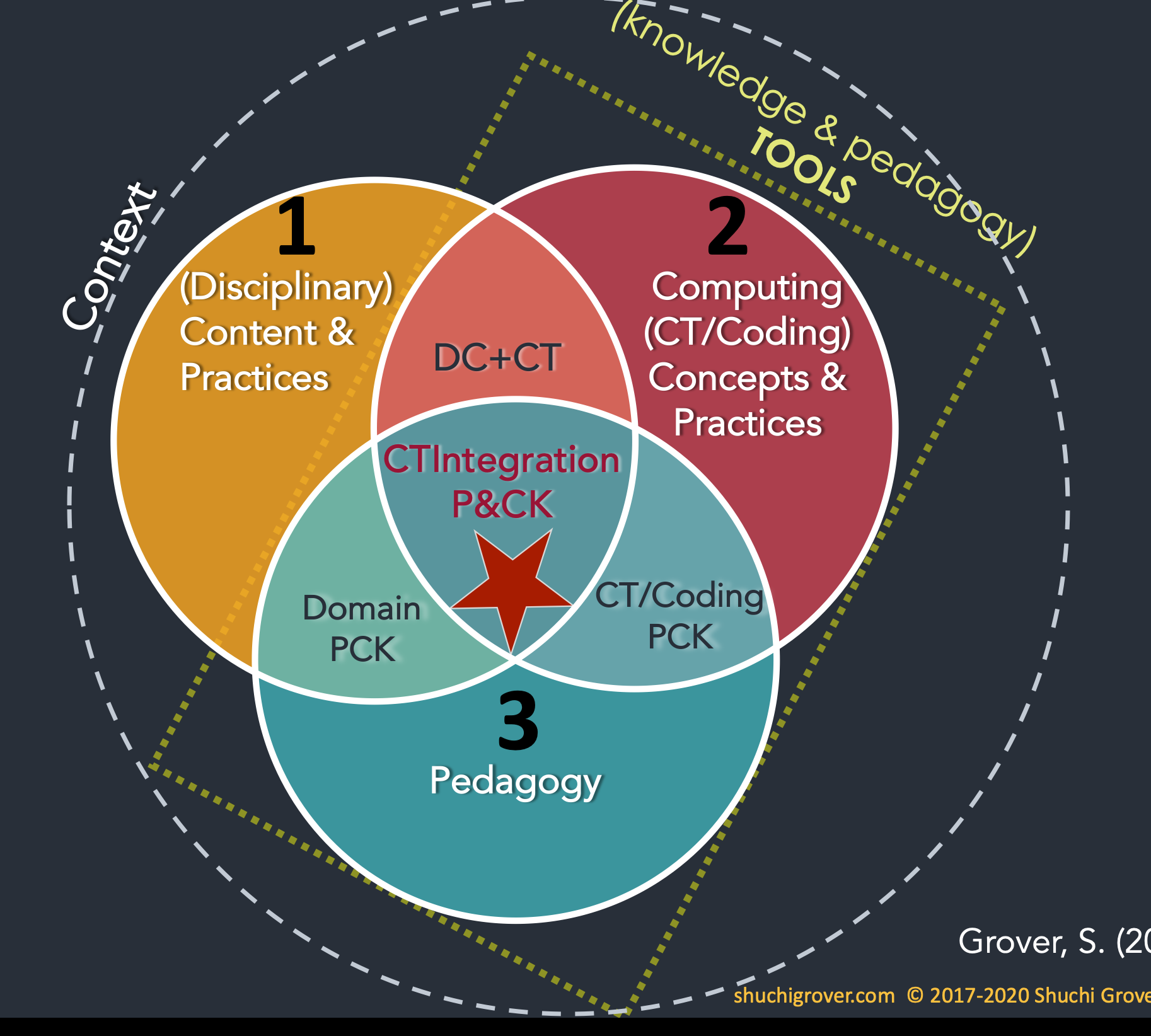
Because we’re talking computing, there is, of course, a close connection with tools for coding and automation (since that is often one of reasons why we integrate). The tool we choose influences both curriculum and pedagogy in the integration context. Tools, as we well know, embody their own pedagogy. The learning philosophy embedded in their design that makes them more or less suitable for different things (remember Dijkstra’s famous quote? “The tools we use have a profound and devious influence on our thinking habits, and therefore on our thinking abilities.”) Programming nvironments may be designed to lower the entry barrier for novices, for example, or for programming in specific domains (like R or MATLAB). And lastly, as with any conceptual framework for learning designs, there is the broader context to keep in mind—the context in which teaching & learning happens, that requires knowledge – not only of the domain or subject and of computing, but also of curriculum standards, and of students and their backgrounds and prior knowledge and the cultural context.
So there you have it, folks! This, in totality, is a framework that I have found to be very useful for thinking about CT/CS integration in subjects that together captures the crucial HOW and WHY and WHAT. This is a theoretical framework about the relationships among the key elements that comprise the integration of CT into a subject and I believe it can catalyze the conceptualization and the practice of CT integration, curriculum & assessment design, as well as teacher preparation.
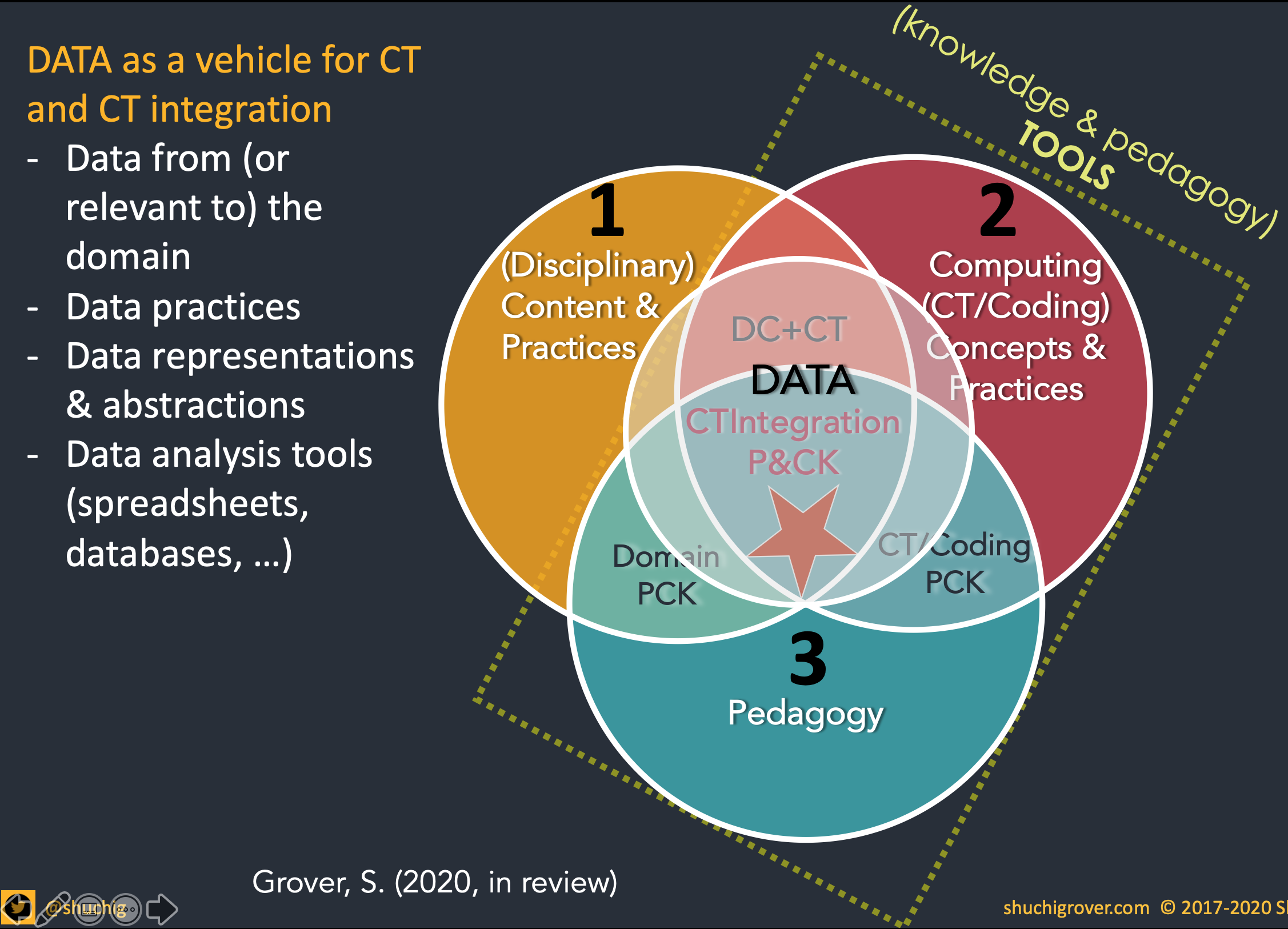
I’d like to point out there is a version of this framework that puts data front and center as a crucial vehicle for integration. These integration contexts mesh well when learning goals include data science, data literacy, data representations, data affordances as key pieces of the CT integration. Examples of data-driven CT integration abound (such as Steven Floyd’s Sports Analytics work, Covitt et al. (2020)’s Comp Hydro project, Bootstrap Data Science, Colby Tofel-Grehl and Kristin Searle’s project that integrates physical computing and data visualizations into social science, the computational journalism example in Grover & Yadav (2020) in the A-Z Handbook on Teaching Programming on using prison population data scraped from public websites using python scripts to interrogate issues of social justice and the criminal justice system.)
In order to understand this framework better, let’s examine some these intersections piecemeal, especially the intersections with CS & CT. First, in addition to the elements seen previously in Lee et al., 2018, the DC+CT integration dimension in this framework also includes guidance on the WHAT of integrating computing into a subject—what topics make for productive integration of computing into a subject? It’s important to remember that not every topic is ripe for integration. We need:
- To exploit synergies, and identify overlaps of domain ideas with CT concepts & practices. This could involve an exercise in standards alignment.
- To identify topics that benefit from creation & making (& leveraging computational power).
- Questions that can be probed and answered with CT/data & data analysis.
- To leverage affordances of computational environments that are synergistic with domain ideas. For example, functional programming & Algebra; Geometry and languages based on turtle geometry like Logo, Scratch, Snap!; Sensors and probes for data collection & analysis in science, geography, social studies.
In terms of CT/CS pedagogy, we have a growing empirical base on how to teach CT/coding—what scaffolds to use, and when and how. We have a (growing) sense for unplugged and plugged approaches (and when to use which), misconceptions & novice difficulties in K-12 computing education, scaffolds & the need for gradual increase in complexity and autonomy, and a growing list of pedagogical approaches such as PRIMM, Use-Modify-Create, TIPP&SEE, worked examples and subgoals, culturally relevant pedagogy, constructionist creation, computational action, and tangible computing. In fact the A to Z Handbook has 12 chapters dedicated to the pedagogy of teaching coding and CT! Different pedagogies may be suitable for different integration contexts. And we also have a sense for what an integration progression might look like.
Some key aspects to keep in mind when designing for CT integration based on this framework are:
- The more tightly these intersections are designed for, the more magical and meaningful the integration (the brighter the star at the center :)).
- Tools & CT tightly intertwined with domain PCK pedagogy can more seamlessly support integration and learning in the domain without integration feeling like a force fit, and something additional for a subject teacher to take on. Examples of this are: functional programming for learning algebraic relationships in Bootstrap, turtle geometry tools (like Scratch and Snap! to support math & spatial thinking, and modeling & simulation environments with support for parameter setup, exploration with parameter sweeping, setting a time-tick, updating variables with time, visualization (of change in variables over time) through data plots.
- The affordances of general purpose languages versus domain-specific languages (e.g. R for Statistics) & domain-specific abstractions (e.g. the “physics blocks” we created in Snap! in our C2STEM project)
- Attending to cognitive load, especially if kids don’t already know coding. Learning to code WHILE coding to learn can be a huge lift (Grover, 2019). The issue of cognitive load is real in integration settings – and #2 and #3 actually help ease cognitive load.
- Explicit bridging to original subject context is needed! (e.g. ScratchMaths does this well)
- Attending to transfer – designing to mediate for transfer and assessing it (Hutchins et al., 2020).
- The importance of framing integration with CT for the learners. I suggest folks check out Conlin et al., 2020 (from our C2STEM project), Brady et al. 2020 (from the JOST Special Issue) and Sengupta et al., 2020 (from the ICLS 2020 symposium).
Since a framework must allow us to develop and identify themes and constructs that apply across diverse cases and examples in various subjects and contexts, I examined a few examples of integration through the analytic lens of this framework — I will share one here — from the C2STEM project that I co-led. I will share other examples as well as the use of this framework for assessment design and teacher preparation in a subsequent post.
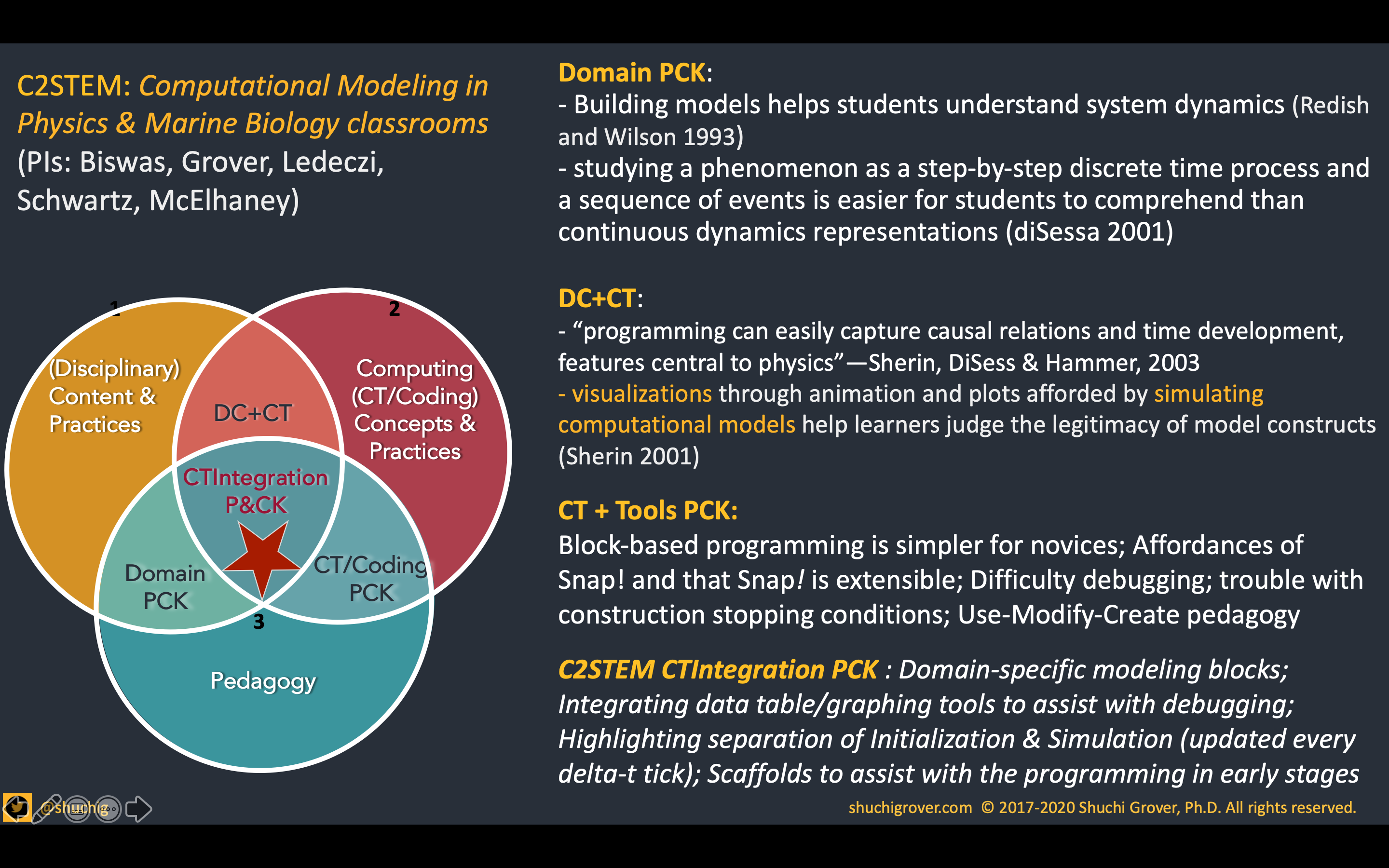
(Hat tip to Koehler & Mishra for their TPACK framework that went a long way in conceptualizing teacher preparation for technology integration. This framework takes inspiration from their work, but the process and purposes and computing context make this distinct, as do the conceptualizations of what those intersections entail.)